Programmation Python pour les scientifiques

Dès que l'on commence à manipuler en Python un grand nombre de données, l'usage de variables devient insuffisant. Exemple : imaginons que l'on veuille stocker les notes des élèves d'une classe pour calculer leur moyenne et leur écart-type. On peut imaginer d'utiliser N variables de type float (N étant le nombre d'élèves de la classe), puis d'écrire des fonctions moyenne() et ecart_type() prenant N paramètres ; fastidieux lorsque N=47, et il faudra la réécrire pour chaque nouvel effectif…

def moyenne47(n1, n2, ..., n47) :
    return (n1 + n2 + ... + n47) / 47.0

En Python, la structure de données qui va nous aider est la liste. C'est un objet de type list qui permet de collecter des éléments : données de type quelconque : int, float, str, bool, d'autres listes, etc.

Exemple :

>>> liste = [1, 2, 3, 'toto']

>>> print liste 
[1, 2, 3, 'toto']

>>> type(liste) 
<type 'list'>

>>> len(liste) 
4

>>> liste[0], liste[1], liste[len(liste) - 1] 
(1, 2, 'toto')

Une liste est créée à l'aide d'une affectation. Ses éléments sont entre crochets […]. La fonction len() prend en argument une liste et retourne son nombre d'éléments. Les éléments d'une liste s'obtiennent grâce à leur indice entre crochets. Attention, le premier élément a pour indice 0 !

Exemple : reprenons notre problème de calcul de la moyenne des notes. Mettons à profit ce que nous avons vu sur les listes ainsi que la fonction sum() qui prend en argument une liste et retourne, lorsque c'est possible, le résultat de l'opération '+' sur ses éléments.

Saisissons la liste des notes :

>>> liste_notes = [10, 12, 14, 6, 8, 15, 3, 17]   # la liste de notes

Définition de la fonction moyenne() qui s'applique à toute liste non vide de nombres :

>>> def moyenne(liste) : # fonction moyenne()
        return sum(liste) / float(len(liste))

>>> moyenne(liste_notes)
 10.625

On obtient le résultat attendu, la moyenne est de 10,625. Sans la conversion en float d'un des arguments de la division, le résultat retourné aurait été 10 (quotient de la division entière) sous Python 2 (mais pas sous Python 3).

Les listes sont des objets modifiables (on dit aussi mutables) : on peut modifier leurs éléments.

>>> liste = [1, 2, 3, 'toto'] # une liste

>>> liste[0] = 'le début'
>>> liste[2] = [-1, -2, -3]
>>> print liste 
['le début', 2, [-1,- 2, -3], 'toto']

>>> print liste[-1], liste[-2]
'toto' [-1, -2, -3]
>>> print liste[-5], liste[4]

IndexError: list index out of range

On modifie un élément de la liste en lui affectant une nouvelle valeur (de n'importe quel type, simple ou complexe). L'indice -1 permet d'obtenir le dernier élément. C'est plus simple que liste[len(liste) - 1]. L'indice -2 permet d'obtenir l'avant-dernier élément, etc. Un indice qui n'est pas compris entre -len(liste) et len(liste)-1 produit une erreur IndexError.

>>> print liste 
['le début', 2, [-1,- 2, -3], 'toto']

>>> type(liste[0]), type(liste[1]), type(liste[2]) 
(<type 'str'>, <type 'int'>, <type 'list'>

>>> print liste[2][0] # liste[2] est une liste 
-1

Les éléments d'une liste sont des valeurs de différents types, celles qu'on lui a affectées.

Une liste de listes permet de constituer un tableau bi-dimensionnel.

>>> l=[['a', 'b'], ['c', 'd']] 
>>> print l[0][0], l[0][1], l[1][0], l[1][1] 
a b c d

Avec un argument entier n, range(n) retourne la liste des n premiers entiers.

>>> print range(10) 
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

Avec deux arguments entiers m, n, range(m,n) retourne la liste des max(0, n−m) entiers consécutifs qui sont compris entre m (inclus) et n (exclu).

>>> print range(0,10)
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> print range(-1,11)
[-1, 0, 1, 2, 3, 4, 5, 6, 7, 8, 10]

Avec trois arguments entiers m, k, n, range(m, n, k) retourne la liste des entiers de la forme kitxmlcodeinlinelatexdvpm+k \cdot pfinkitxmlcodeinlinelatexdvp, avec p entier naturel, et qui sont compris entre m (inclus) et n (exclu).

>>> print range(0, 10, 2)
[0, 2, 4, 6, 8]
>>> print range(10,0,-2)
[10, 8, 6, 4, 2]

Un argument non entier provoque un message d'erreur TypeError.

L'instruction for permet de répéter une séquence d'instructions, en boucle, pour une variable qui décrit une liste d'éléments.

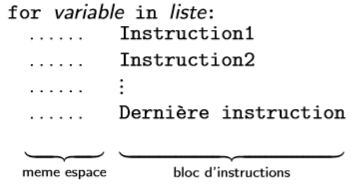
On l'écrit en langage algorithmique :

Pour tout i dans liste faire : 
     Instruction 1
     ...
     Instruction N

Bien sûr la variable i peut apparaître dans le bloc d'instructions (comme variable locale : c'est une « copie », la modifier n'affecte pas la liste).

for i in liste : 
    # instruction 1
    # ...
    # instruction N

produit un résultat identique à la boucle while :

L = len(liste)    # L est la longueur de la liste
j = 0             # j est l'indice
while (j < L) :   # tant que l'indice ne dépasse pas 
    i=liste[j]    # i est l'élément d'indice j
    # instruction 1
    # ...
    # instruction N
    j = j + 1     # incrémenter l'indice j

Une boucle while est plus générale. On a le droit de modifier la longueur de la liste dans la boucle while ; on n'en a pas le droit dans la boucle for (on peut toujours modifier les éléments de la liste). Dans une boucle for, le nombre de répétitions de la boucle est fixée à l'entrée dans la boucle, ici c'est len(liste).

I-D-1. Exemple 1 : liste des carrés▲

>>> liste_vide=[ ]
>>> liste_vide.append('toto')
>>> print liste_vide
['toto']
>>> liste_vide.append('le héros') 
>>> print liste_vide
['toto', 'le héros']

>>> liste_carres = [ ]              # initialisation 
>>> for i in range(21) :
        liste_carres.append(i ** 2) # actualisation

>>> print liste_carres
[0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225, 256, 289, 324, 361, 400]

I-D-2. Exemple 2 : la suite de Fibonacci▲

>>> def fibonacci(N) :
        result = [0, 1] # Initialisation
        for k in range(2, N) :
            result.append(result[k - 1] + result[k - 2])
        return result

>>> fibonacci(16)
[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610]

I-D-3. Exemple 3 : calcul intégral - méthode des trapèzes▲

Soit l'application kitxmlcodeinlinelatexdvpf\,:\,x\mapsto x^2finkitxmlcodeinlinelatexdvp définie sur kitxmlcodeinlinelatexdvp\mathbb{R}^2finkitxmlcodeinlinelatexdvp.

Écrire une fonction trapeze() qui prend en argument deux réels kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp et retourne une approximation de l'intégrale de kitxmlcodeinlinelatexdvpffinkitxmlcodeinlinelatexdvp de kitxmlcodeinlinelatexdvpafinkitxmlcodeinlinelatexdvp à kitxmlcodeinlinelatexdvpbfinkitxmlcodeinlinelatexdvp par la méthode des trapèzes. Comparer son résultat avec la valeur quasi-exacte.

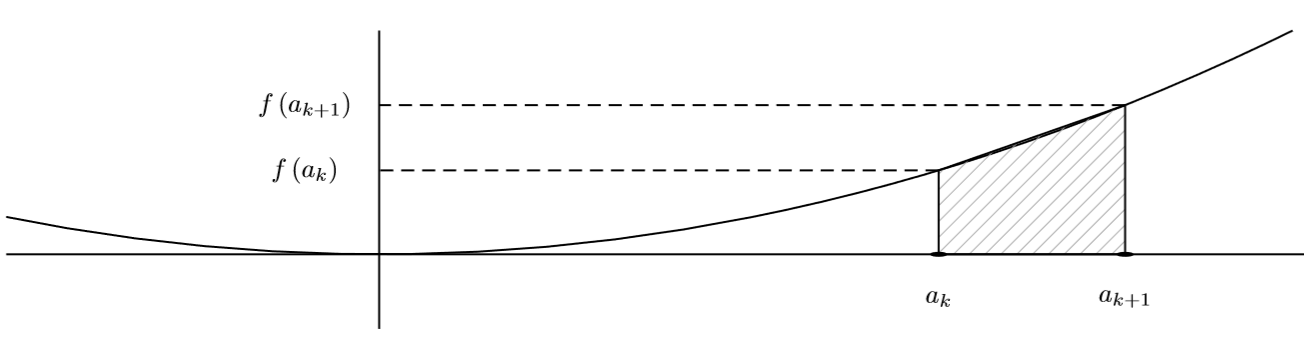
Méthode des trapèzes : si kitxmlcodeinlinelatexdvpf\,:\, [a;\,b] \longrightarrow\mathbb{R}finkitxmlcodeinlinelatexdvp est continue,

soit kitxmlcodeinlinelatexdvpa_k = a+k\dfrac{b-a}{n}\,\mathrm{pour}\,k\in[[0;\,n]]finkitxmlcodeinlinelatexdvp (ainsi kitxmlcodeinlinelatexdvpa_0=a, a_n=bfinkitxmlcodeinlinelatexdvp). Si kitxmlcodeinlinelatexdvpnfinkitxmlcodeinlinelatexdvpest assez grand :

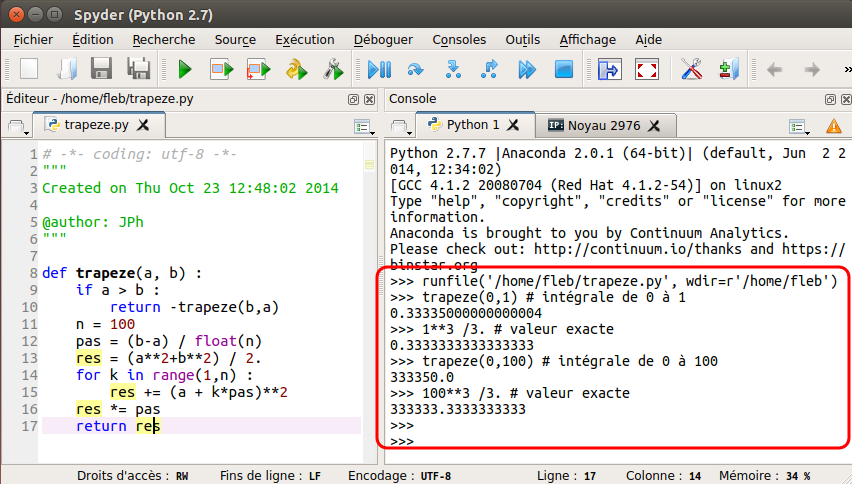
kitxmlcodelatexdvp\begin{aligned} \int^b_a f(x)\textrm{d}x&\approx\left(\dfrac{b-a}{n}\right)\sum^{n-1}_{k=0} \dfrac{f(a_k)+f(a_{k+1})}{2}\\ &\approx \left(\dfrac{b-a}{n}\right)\left( \dfrac{f(a)+f(b)}{2}+\sum^{n-1}_{k=1} f(a_k)\right) \end{aligned}finkitxmlcodelatexdvp

Cliquez sur l'icône .

Méthode des trapèzes

Cacher/Afficher le codeSélectionnez

def trapeze(a, b) : 
    if a > b :
        return -trapeze(b,a) 
    n = 100 
    pas = (b-a) / float(n) 
    res = (a**2+b**2) / 2. 
    for k in range(1,n) : 
        res += (a + k*pas)**2
    res *= pas 
    return res

la boucle for permet de calculer la somme.

• L'instruction '+=' : a += b donne le même résultat que a = a + b. Elle lui est préférable, car plus rapide : dans le premier cas, la valeur de b vient s'ajouter à celle de a, dans le deuxième, les valeurs de a et b sont d'abord dupliquées en mémoire avant d'être additionnées entre elles puis le résultat est affecté à la variable a. On dispose aussi des opérateurs : '-=', '*=', '\=', etc.

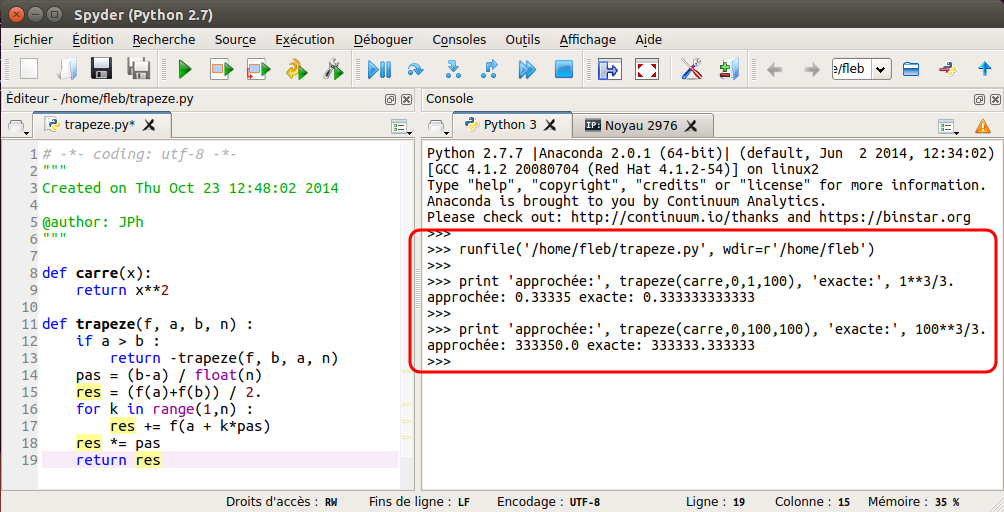
On peut améliorer la fonction en prenant la fonction à intégrer et le pas en paramètres : trapeze(f, a, b, n).

La fonction à intégrer est définie par :

 

Sélectionnez

def carre(x) :
    return x**2

Cliquez sur l'icône .

 

Cacher/Afficher le codeSélectionnez

def carre(x):
    return x**2

def trapeze(f, a, b, n) : 
    if a > b :
        return -trapeze(f, b, a, n) 
    pas = (b-a) / float(n) 
    res = (f(a)+f(b)) / 2. 
    for k in range(1,n) : 
        res += f(a + k*pas)
    res *= pas 
    return res

À l'exécution :