Programmation Python pour les scientifiques - Premier contact -

Python est un langage multiparadigme permettant la programmation impérative, structurée, orientée objet, de haut niveau. Il présente les avantages suivants :

• Sa syntaxe est très simple et concise : « on code comme on pense ». Donc facile à apprendre. Proche du langage algorithmique.
• Moderne. Très largement répandu dans l'industrie, l'enseignement et la recherche, notamment pour ses applications scientifiques. Une large communauté participe à son développement.
• Puissant, muni de nombreuses bibliothèques de fonctions dont de très bonnes bibliothèques scientifiques.
• Pratique pour travailler sur des objets mathématiques. Assez proche du langage mathématique.
• Gratuit, disponible sur la plupart des plates-formes (Windows, Mac, Linux).

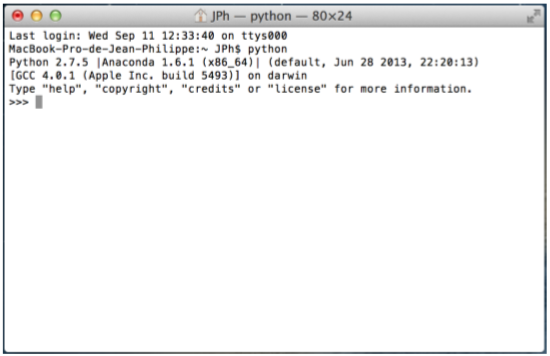
Python est un langage interprété qui peut être utilisé en mode console, c'est-à-dire avec une interface en ligne de commande. Lancer une fenêtre de console et simplement taper la commande 'python' à l'invite, suivie de la touche <Entrée>.

Une invite de commande (ou prompt), symbolisée ici par : >>>, apparaît. On peut y saisir tout type de commandes Python :

>>> print ('bonjour !')

Une commande saisie au prompt est passée à l'interpréteur Python lorsque l'on presse la touche <Entrée> :

>>> print ('bonjour !')
bonjour !
>>>

La commande print() écrit à l'écran une chaîne de caractères, c'est-à-dire une suite de caractères alphanumériques compris entre apostrophes ' ' ou guillemets anglais doubles " " :

>>> print ('bonjour ! \nMPSI1')
bonjour ! 
MPSI1
>>>

Le caractère spécial \n permet un saut de ligne.

Python peut se comporter comme une calculatrice :

>>> 2*3 - 1
5
>>>

Il respecte l'ordre usuel des opérations :

>>> 2*(3 - 1)
4
>>>

Et comprend les opérations sur les nombres à virgule flottante de type float :

>>> 3*(-1.5)
-4.5
>>>

La mise en puissance s'obtient grâce à l'opérateur ** :

>>> 3**2
9
>>>

L'exposant peut être réel. Ainsi, l'opérateur **0.5 extrait la racine carrée :

>>> 2**0.5
1.4142135623730951
>>> 2**-0.5
0.7071067811865476
>>>

Lorsque y n'est pas entier, x^y n'est défini que pour x > 0 :

>>> (-2)**0.5

Traceback (must recent call last) :
   file "<stdin>", line 1, in <module>
ValueError: negative number can't be raised to a fractionnal power

Attention, sous Python 2 le symbole de division / a une signification ambiguë, selon que les opérandes sont de type int (entier), ou de type float (nombre à virgule flottante).

Si au moins un des deux opérandes est un nombre réel à virgule flottante, la division avec le symbole / fonctionne comme la « vraie » division :

>>> 3.0 / 2
1.5
>>> 3 / 2.0
1.5
>>> 3. / 2
1.5
>>> 3 / 2.
1.5
>>>

Dans les deux derniers cas précédents, on force le type d'un des deux opérandes en float en ajoutant un point décimal :

>>> type(3)
<type 'int'>
>>> type(3.)
<type 'float'>
>>>

Par contre :

>>> 3 / 2
1
>>>

Les deux opérandes sont des entiers (int), la division avec / retourne alors le quotient entier de la division euclidienne. Ce comportement (déroutant a priori) est propre aux versions 2.x de Python.

Il faudra prendre en compte ce comportement particulier de Python 2 qui peut conduire à des erreurs si votre programme s'attend à des opérandes de type float, mais que les valeurs entières sont aussi possibles.

>>> a = 10
>>> b = 6
>>> a / b
1
>>> (a*1.)/b    # le numérateur forcé en float
1.6666666666666667
>>>

Note : les commentaires sont placés après un croisillon # . Tout ce qui est placé après le caractère # sur une ligne est ignoré par l'interpréteur. Il est essentiel de les utiliser lors de l'écriture d'un programme.

Si vous voulez éviter ce genre de contorsion dans vos programmes, vous importez la classe division du module __future__ une fois pour toutes en début de programme pour obtenir de « vraies » divisions dans tous les cas :

>>> from __future__ import division
>>> 10 / 6
1.6666666666666667

On utilisera l'opérateur spécifique // pour obtenir le quotient entier de la division euclidienne. Alors qu'avec l'opérateur modulo %, on obtient le reste de la division euclidienne :

n = [n/m] x m + n%m

>>> 10 // 6
1
>>> 10 % 6
4

Par défaut, Python dispose bien de quelques fonctions natives pour faire des maths, mais il n'est pas très doué dans ce domaine :

>>> # Sans bibliothèque, Python est ignorant en trigo par exemple
>>> cos(0)

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
    cos(0)
NameError: name 'cos' is not defined

>>> pi

Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
    pi
NameError: name 'pi' is not defined

Pas de trigonométrie avec les fonctions natives de Python ! Vous pouvez voir la liste des fonctions intégrées (built-in Functions) dans la documentation officielle.

Pour aller plus loin, il suffit de faire appel au module standard math de fonctions mathématiques prédéfinies :

>>> from math import * # importation de toutes les fonctionnalités du module
>>> pi
3.141592653589793
>>> cos(pi)
-1.0
>>> acos(-1)
3.141592653589793
>>>

>>> sqrt(2)                    # racine carrée (sqrt = square root)
1.4142135623730951
>>> e
2.718281828459045
>>> log(e)                     # logarithme népérien
1.0
>>> exp(1)                     # exponentielle
2.718281828459045
>>> log(256,2)                 # logarithme base 2
8.0
>>> log(1000,10)               # logarithme base 10
2.9999999999999996
>>> # lui préférer :
>>> log10(1000)                # logarithme base 10 plus précis
3.0
>>> fabs(-3)                   # valeur absolue de type float
3.0
>>> floor(pi)                  # Retourne l'entier le plus proche (en float), inférieur ou égal au réel passé en paramètre 
3.0
>>> floor(-pi)                 # alors que int(-pi)=-3
-4.0

Le module fractions permet le calcul sur les fractions.

Cet exemple se passe de commentaires :

>>> # le module fraction
>>> 1/3 + 2/5
0.7333333333333334
>>> from fractions import Fraction
>>> Fraction(1, 3) + Fraction(2, 5)
Fraction(11, 15)
>>>

Ici l'instruction from fractions import Fraction n'importe que la classe Fraction du module fractions. On peut aussi importer toutes les fonctionnalités d'un module en écrivant : from fractions import *.

L'utilisateur peut définir ses propres fonctions :

>>> def ma_fonction(x):
        return x**2 - 2*x + 1

>>> ma_fonction(1)
0
>>> ma_fonction(0)
1
>>>

Ici l'appel de ma_fonction(x) retourne kitxmlcodeinlinelatexdvpx^2 ? 2x + 1 \vphantom{y}finkitxmlcodeinlinelatexdvp grâce à l'instruction return. On peut ne pas mentionner de valeur de retour dans une fonction, implicitement elle retourne None et on peut alors parler de procédure :

>>> # Définition d'une procédure (pour Python c'est une fonction qui retourne None)
>>> def ma_procedure(x):
        print ("L'image par ma_fonction de", x , "est", ma_fonction(x))

>>> ma_procedure(1)

L'image par ma_fonction de 1, est 0

>>> ma_procedure(0)

L'image par ma_fonction de 0, est 1

>>> ma_procedure(10)

L'image par ma_fonction de 10, est 81

Notez qu'une fonction peut être appelée dans la définition d'une autre fonction.

Syntaxe pour la définition d'une fonction :

def nom_fonction(parametre1, parametre2, ...) :
.... Instruction 1
.... Instruction 2
.... ...
.... Instruction n

L'instruction def permet de définir une fonction informatique. Elle est suivie du nom de la fonction, suivi d'une liste de paramètres entre parenthèses. La parenthèse fermante est suivie de deux points ':' et d'un bloc d'instructions. Elles doivent toutes être décalées du même nombre d'espaces (en général, 4). Appuyer sur <Entrée> à l'invite de commande pour achever la définition.

Note : dans le langage Python, chaque fois que vous terminez une ligne d'instruction par le signe deux-points ( ': ' ), le retour à la ligne suivante implique l'écriture d'un bloc d'instructions. En Python, un bloc d'instructions se caractérise toujours par le même niveau d'indentation (nombre d'espaces blanches ou de tabulations en début de ligne). Le simple fait de changer de niveau d'indentation signifie que vous sortez d'un bloc d'instructions donné. Exemple :

if mon_parametre is None:
    # bloc d'instructions
    print("mon paramètre est None")
    # le bloc continue ici
    mon_parametre = 0
# ici, on change d'indentation
# donc on sort du bloc précédent
print("ce code ne fait pas partie de la condition précédente.")

• La notion de variable est essentielle en programmation.
• Elle permet de stocker en mémoire des valeurs, de les utiliser et de les modifier à volonté au sein d'un programme.
• La valeur d'une variable évolue au cours de l'exécution d'un programme, en fonction du déroulement du programme et selon ses instructions.

Quelques exemples de variables de types entier int, réel à virgule flottante float et chaîne de caractères str.

>>> # exemple de variables
>>> rayon_cercle = 12               # variable rayon_cercle de type entier
>>> pi = 3.14159                    # variable pi de type float
>>> mon_texte = "calcul de l'aire d'un disque"     # variable mon_texte de type str

Avec l'instruction print(), il n'est pas nécessaire de convertir les expressions et/ou les variables en chaînes de caractères, cette conversion est implicite, elle s'effectue de manière totalement transparente pour l'utilisateur. Il suffit donc d'utiliser l'expression et/ou la variable dans print() telle quelle, sans autre forme de procès.

>>> print rayon_cercle
12
>>> print mon_texte
calcul de l'aire d'un disque
>>> print "Aire du disque :", pi*rayon_cercle**2
Aire du disque : 452.38896
>>>

L'opération principale pour une variable est l'affectation représentée par le symbole =.

>>> rayon_cercle = 12.
>>> print rayon_cercle
12.0
>>> diametre_cercle = 2.*rayon_cercle
>>> print diametre_cercle
24.0
>>>

Une variable est une donnée que l'ordinateur va stocker dans un espace mémoire. Elle est caractérisée par :

• un identificateur : pour nous c'est son nom, qui permet de manipuler la variable au sein d'un programme ou d'une instruction (en mode console). C'est une chaîne de caractères alphanumériques, c.-à.-d. composée de lettres et de chiffres, qui ne doit pas débuter par un chiffre. Évitez les lettres majuscules et les caractères accentués. Préférez des noms de variable explicites en lettres minuscules, les mots séparés par un caractère underscore '_' (voir les recommandations de la documentation officielle) ;
• un type : entier int, réel à virgule flottante float, chaîne de caractères str, booléen, etc. ;
• un contenu : c'est sa valeur. Elle est stockée dans la mémoire centrale sous forme d'un nombre en écriture binaire.

En Python la définition (déclaration) d'une variable se fait à l'aide d'une affectation :

>>> # Définition et affectation d'une variable  nombre_vies
>>> nombre_vies = 3
>>> type(nombre_vies)   # type de la variable nombre_vies
<type 'int'>

Python pratique le typage dynamique : il n'est pas utile (contrairement à d'autres langages) de déclarer le type de la variable, Python s'en charge.

>>> temperature = 23.    # le point décimal force le type à float
>>> type(temperature)
<type 'float'>

Le type d'une variable peut être modifié en cours de route… C'est toutefois une pratique à déconseiller vivement !

Python permet en une seule affectation ('=') de déclarer plusieurs variables :

>>> # Affectation multiple
>>> temperature, texte_intro = 12.5, "bonjour"
>>> temperature
12.5
>>> texte_intro
'bonjour'
>>>

Les variables à gauche de l'opérateur d'affectation ('=') sont séparées par des virgules, de même que les valeurs à droite de '=', et sont affectées de gauche à droite.

Exemple : calcul des premiers termes de la suite de Fibonacci :

>>> # Calcul des premiers termes de la suite de Fibonacci
>>> u, v = 0, 1
>>> print u, v
0 1

>>> u, v = u+v, u+2*v
>>> print u, v
1 2
>>> u, v = u+v, u+2*v
>>> print u, v
3 5
>>> u, v = u+v, u+2*v
>>> print u, v
8 13
>>> u, v = u+v, u+2*v
>>> print u, v
21 34
>>>

La touche ? du clavier (déplacement vers le haut) permet de naviguer dans l'historique de commandes et de relancer une ligne d'instruction précédente.

Bien noter que durant une affectation multiple les valeurs (à droite du =) sont celles avant l'appel de l'instruction.

Ainsi l'instruction a, b = b, a échange les valeurs de deux variables a et b :

>>> # Échange des valeurs de deux variables
>>> a, b = 1, 2
>>> print a, b
1 2
>>> a, b = b, a
>>> print a, b
2 1
>>>

Dans d'autres langages pour échanger les valeurs de deux variables, il faut faire appel à une fonction prédéfinie (souvent swap(.,.)), ou procéder en plusieurs affectations.

À l'aide d'une variable temporaire :

>>> a, b = 1, 2
>>> vartemp = b
>>> b = a
>>> a = vartemp
>>> print a, b
2 1
>>>

Sans variable temporaire :

>>> a, b = 1, 2
>>> a = a + b
>>> b = a - b
>>> a = a - b
>>> print a, b
2 1
>>>

Il faut tout de même trois affectations, et le code n'est pas facilement lisible…

Existence : par division euclidienne kitxmlcodeinlinelatexdvp\exists !\ (q_0,u_0) \in \mathbb{N}^2finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvpn=q_0\times m+u_0\,\mathrm{ et }\, 0\leq u_0 < mfinkitxmlcodeinlinelatexdvp. Si kitxmlcodeinlinelatexdvpq_0=0finkitxmlcodeinlinelatexdvp la suite kitxmlcodeinlinelatexdvpu_0finkitxmlcodeinlinelatexdvp convient puisque kitxmlcodeinlinelatexdvpn=u_0\times m^0finkitxmlcodeinlinelatexdvp.

Si kitxmlcodeinlinelatexdvpq_0\neq0finkitxmlcodeinlinelatexdvp alors par la division euclidiennekitxmlcodeinlinelatexdvp\exists !\ (q_1,u_1) \in \mathbb{N}^2\,\mathrm{avec}\,q_0=q_1\times m+u_1 \,\mathrm{et}\, 0\leq u_1 <mfinkitxmlcodeinlinelatexdvp.

Remarquer que kitxmlcodeinlinelatexdvpn>q_0>q_1finkitxmlcodeinlinelatexdvp puisque kitxmlcodeinlinelatexdvpm>1finkitxmlcodeinlinelatexdvp. Ainsi en poursuivant ce procédé on construit une suite finie kitxmlcodeinlinelatexdvp(u_0,\,u_1,\cdots,u_N)finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvp0 \leq u_i <m,\ q_N=0 \vphantom{y}finkitxmlcodeinlinelatexdvp et :

Unicité. Elle provient de l'unicité du quotient et du reste dans la division euclidienne : si kitxmlcodeinlinelatexdvpn= \sum^N_{i=0} u_i \times m^ifinkitxmlcodeinlinelatexdvp alors le procédé précédent produit la suite kitxmlcodeinlinelatexdvp(u_0,\,u_1,\cdots,u_N)finkitxmlcodeinlinelatexdvp.

Exemple : écriture de 72 en base 2 :

72 s'écrit 1001000 en base 2 (binaire).

En Python :

Python dispose d'une fonction intégrée bin(x) qui règle le problème :

>>> bin(72)
'0b1001000'

À titre d'exercice, on peut tenter une solution à partir d'une boucle while :

a=72
>>> while a>0 :
        print a%2
        a=a//2  # division entière
0
0
0
1
0
0
1

L'instruction while répète en boucle le bloc d'instructions qui lui est rattaché tant que l'expression conditionnelle vaut True (évaluation booléenne de l'expression à vrai).

Exemple : écriture de 72 en base 16 :

72 s'écrit 48 en base 16 (ou hexadécimal).

En Python :

là aussi, Python dispose d'une fonction intégrée hex(x) performante et qui règle le problème :

>>> hex(72)
'0x48'

Mais pour le fun, on peut connencer l'aventure avec while :

a = 72
>>> while a :
        print a%16
        a = a//16   # division entière
8
4

Pour écrire un nombre en base 16 on utilise les « chiffres » de 0 à 9 et A=10, B=11, C=12, D=13, E=14, F=15.

En 2 chiffres on écrit tous les nombres de 0 à FF = 15 + 15 x 16 = 16^2 ? 1 = 255. Autant qu'en binaire avec 8 bits (ou chiffre 0,1), puisque 11111111 = 2^8 ? 1 = 255.

Puisque 2⁴ = 16 on a la conversion binaire/hexadécimal :

• 0000=0, 0001=1, 0010=2, 0011=3, 0100=4, 0101=5, 0110=6, 0111=7, 1000=8, 1001=9, 1010=A, 1011=B, 1100=C, 1101=D, 1110=E, 1111=F.

Exemple : 72₁₀ = 0100 1000₂ = 48₁₆.