Programmation Python pour les scientifiques

Il existe de nombreux modules scientifiques sous Python :

• NumPy : puissant outil pour créer, manipuler, et appliquer de nombreuses opérations sur des tableaux de nombres (matrices). Stable et bien documenté ;
• SciPy : fonctions mathématiques puissantes s'appliquant aux tableaux générés par NumPy. C'est la boîte à outil numérique pour les tableaux NumPy. Elle contient des opérations spécifiques (algèbre linéaire, statistique…) de manipulation de tableaux, de plus haut niveau que celles de NumPy ;
• matplotlib : permet le tracé de graphes de fonctions.

Nous allons voir de plus près les modules NumPy et matplotlib.

Le module NumPy permet de créer, de manipuler, des tableaux de nombres, ou matrices, et de leur appliquer des opérations mathématiques courantes.

La fonction array() permet de créer un tableau, ou array, à partir d'un tableau Python c'est-à-dire d'une liste de listes de nombres (de même longueur) :

>>> import numpy as np
>>> A = np.array([[1,1,1],[0,1,1],[0,0,1]])
>>> A
 array([[1, 1, 1],
        [0, 1, 1],
        [0, 0, 1]])
>>> print A
[[1 1 1]
 [0 1 1]
 [0 0 1]]

La fonction arange() crée une matrice ligne de façon assez analogue à la façon dont range() crée une liste, à ceci près que les coefficients ne sont pas forcément entiers :

>>> v = np.arange(0, 1.5, 0.5)
>>> v
array([ 0., 0.5, 1. ])
>>> 2*v
array([ 0., 1., 2. ])
>>> -2*v + 10
array([ 10., 9., 8. ])

On peut appliquer sur les tableaux de nombreuses opérations arithmétiques, certaines étant comprises terme à terme.

On accède aux éléments d'un tableau comme en Python, grâce à un indice entre crochets :

>>> A[0], A[1]
(array([1, 1, 1]), array([0, 1, 1]))
>>> A[1][0]
0

On peut échantillonner (slicing) :

>>> A[0:1]
array([[1, 1, 1]])
>>> A[::-1]
array([[0, 0, 1],
       [0, 1, 1],
       [1, 1, 1]])

Le type d'une matrice s'obtient grâce à la fonction shape(), son nombre d'éléments grâce à size(). La fonction reshape() permet de changer la forme (=type) d'une matrice :

>>> L=np.arange(0,10)
>>> np.size(L)
10
>>> np.reshape(L,(2,5))
array([[0, 1, 2, 3, 4],
       [5, 6, 7, 8, 9]])
>>> L
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
>>> M = np.reshape(L,(2,5)) ; np.shape(M)
(2, 5)

Le produit matriciel s'obtient à l'aide de la fonction dot(). Si le deuxième argument est une matrice ligne, dot() la traitera si besoin est comme une matrice colonne, ou vecteur, en la transposant. C'est en effet plus pratique de saisir v= np.arange(0,3) ou v=array([0, 1, 2]) que v=array([[0],[1],[2]]).

Exemple : avec kitxmlcodeinlinelatexdvpA= \begin{pmatrix}1 & 1 & 1\\ 0 & 1 & 1\\ 0 & 0 & 1\end{pmatrix}finkitxmlcodeinlinelatexdvp et kitxmlcodeinlinelatexdvpv=\begin{pmatrix}0 & 1 & 2\end{pmatrix}finkitxmlcodeinlinelatexdvp.

Le produit kitxmlcodeinlinelatexdvpA \times vfinkitxmlcodeinlinelatexdvp n'est pas défini ; le produit kitxmlcodeinlinelatexdvpv \times A \,=\begin{pmatrix}0 & 1 & 3\end{pmatrix}finkitxmlcodeinlinelatexdvp. Le produit kitxmlcodeinlinelatexdvpA \, \times ^t v \,= \begin{pmatrix}3\\ 3\\ 2\end{pmatrix}finkitxmlcodeinlinelatexdvp.

Voilà ce que dot() retourne :

>>> np.dot(A,v)
array([3, 3, 2])
>>> np.dot(v,A)
array([0, 1, 3])

On le voit, lorsque la multiplication est impossible, pour kitxmlcodeinlinelatexdvpA \times vfinkitxmlcodeinlinelatexdvp, la fonction effectue kitxmlcodeinlinelatexdvpv \, \times ^t Afinkitxmlcodeinlinelatexdvp, qui a retourné pour résultat kitxmlcodeinlinelatexdvp\begin{pmatrix}3 & 3 & 2\end{pmatrix}finkitxmlcodeinlinelatexdvp.

On pourra saisir les « vecteurs » sous forme de matrice ligne (leur transposée). Ce fonctionnement est commun aux logiciels de calcul sur des matrices (Matlab et Scilab).

Pour effectuer le produit scalaire de deux « vecteurs », utiliser la fonction vdot().

La fonction transpose() permet d'obtenir la transposée :

>>> np.transpose(A)
array([[1, 0, 0],
       [1, 1, 0],
       [1, 1, 1]])

La transposée d'un « vecteur » est encore un « vecteur ».

Attention, l'opération A ** 2 correspond à une élévation au carré terme à terme :

>>> A ** 2
array([[1 1 1]
       [0 1 1]
       [0 0 1]])
>>> (2*A) ** 2
array([[4 4 4]
       [0 4 4]
       [0 0 4]])

Pour élever A au carré, faire plutôt :

>>> np.dot(A,A)
array([[1, 2, 3],
       [0, 1, 2],
       [0, 0, 1]])

Pour élever une matrice carrée A à une puissance n :

>>> B = A
>>> for i in range(1,n):
        B = np.dot(A,B) # à la sortie de boucle B contient A^n

De même l'inversion A ** -1 se fait terme à terme. Elle produira ici une erreur (division par 0) alors même que la matrice A est inversible.

Certaines fonctions plus spécifiques sont disponibles dans un sous-module. Pour l'algèbre linéaire. C'est le sous-module linalg de NumPy. Toutes les fonctions de ce sous-module devront être saisies avec le préfixe np.linalg.

Pour l'inversion de matrice : utiliser la fonction inv() du sous-module linalg :

>> np.linalg.inv(A)
array([[ 1., -1., 0.],
       [ 0., 1., -1.],
       [ 0., 0., 1.]])

Le sous-module linalg contient aussi, entre autres :

1. La fonction det() qui retourne le déterminant d'une matrice ;
2. La fonction solve(A, b) qui résout le système linéaire de matrice A et de second membre b (vecteur ou ligne).

Exemple : résoudre le système linéaire :

Solution : cliquez sur l'icône pour dévoiler le code.

>>> A = np.array([[1,-1,1], [-1,1,1], [2,-1,-1]])
>>> b = np.array([1,1,0])
>>> np.linalg.solve(A, b) # avec solve()
array([ 1., 1., 1.])
>>> np.dot(np.linalg.inv(A), b) # en inversant A
array([ 1., 1., 1.])

NumPy contient aussi constantes et fonctions mathématiques usuelles.

Pour le simple tracé de courbes, nous n'utiliserons que le sous-module pyplot importé, avec alias, à l'aide de la commande :

>>> import matplotlib.pyplot as pp

Voir la documentation Matplotlib.

● Les fonctions essentielles de pyplot sont :

• plot() pour le tracé de points, de courbes ;
• show() pour afficher le graphique créé.

● Utiliser plot() avec :

• en premier argument la liste des abscisses ;
• en deuxième argument la liste des ordonnées ;

• en troisième argument (optionnel) le motif des points :

  • '.' pour un petit point,
  • 'o' pour un gros point,
  • '+' pour une croix,
  • '*' pour une étoile,
  • '-' points reliés par des segments,
  • '--' points reliés par des segments en pointillés,
  • '-o' gros points reliés par des segments (on peut combiner les options),
  • 'b', 'r', 'g', 'y' pour de la couleur (bleu, rouge, vert, jaune, etc.).

Voir la documentation pyplot.

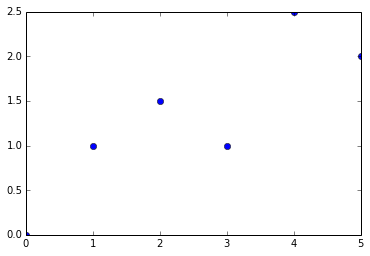
Exemple : pour le tracé d'un nuage de points, le code saisi en ligne de commande suivant

>>> import matplotlib.pyplot as pp
>>> abs = [0, 1, 2, 3, 4, 5]
>>> ord = [0, 1, 1.5, 1, 2.5, 2]
>>> pp.plot(abs, ord, 'o')
[<matplotlib.lines.Line2D object at 0x10c6610d0>]
>>> pp.show()

va produire un graphique (au format .png) :

Exemple : pour le tracé d'une ligne brisée :

>>> import matplotlib.pyplot as pp
>>> abs = [n/2. for n in range(10)]
>>> ord = [n % 2 for n in range(10)]
>>> pp.plot(abs,ord,'-b')
[<matplotlib.lines.Line2D object at 0x10dd1fa10>]
>>> pp.show()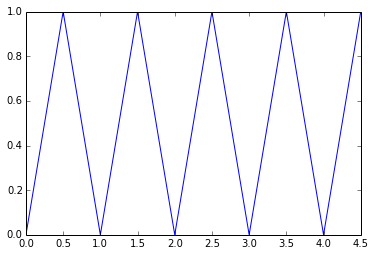

Exemple : pour le tracé de courbes représentatives de fonctions réelles :

>>> import matplotlib.pyplot as pp
>>> import numpy as np # pour linspace() et les fonctions mathématiques
>>> X = np.linspace(0, 2*np.pi, 256) # X = 256 pts régulièrement espac#es
>>> Ycos = np.cos(X) # image directe de X par cos
>>> Ysin = np.sin(X) # image directe de X par sin
>>> pp.plot(X,Ycos,'b') # tracé de la courbe de cos en bleu
[<matplotlib.lines.Line2D object at 0x10d5e2b50>]
>>> pp.plot(X,Ysin,'r') # tracé de la courbe de sin en rouge
[<matplotlib.lines.Line2D object at 0x1073aad90>]
>>> pp.show()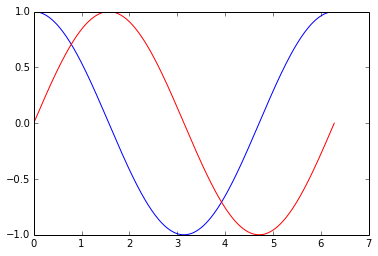

On améliore le tracé en remplissant quelques options avant de le sauvegarder (au format .png dans le répertoire utilisateur).

>>> pp.plot(X, Ycos, 'b', X, Ysin, 'r') # Tracé simultané des deux courbes
>>> pp.grid(True) # Affiche la grille
>>> pp.legend(('cos','sin'), 'upper right', shadow = True) # Légende
>>> pp.xlabel('axe des x') # Label de l'axe des abscisses
>>> pp.ylabel('axe des y') # Label de l'axe des ordonnées
>>> pp.title('Fonctions cosinus et sinus') # Titre
>>> pp.savefig('ExempleTrace') # sauvegarde du fichier ExempleTrace.png
>>> pp.show()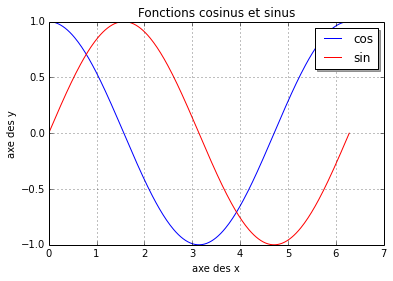

On peut tout aussi bien tracer des courbes paramétrées :

>>> T = np.linspace(0,2*np.pi,256) # paramètre t
>>> X = [ t * np.cos(t) for t in T ] # x(t) = t.cos(t)
>>> Y = [ t * np.sin(t) for t in T ] # y(t) = t.sin(t)
>>> pp.plot(X,Y,'b') # Tracé de la courbe paramétrée {(x(t),y(t))}
[<matplotlib.lines.Line2D object at 0x10c044ed0>]
>>> pp.show()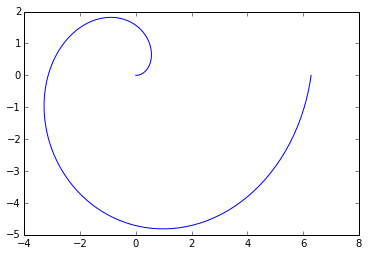

Exemple : tracé du cercle unitaire :

>>> T = np.linspace(0,2*np.pi,256) # paramètre t
>>> X = np.cos(T) # x(t) = cos(t)
>>> Y = np.sin(T) # y(t) = sin(t)
>>> pp.plot(X,Y,'b') # Tracé de la courbe paramétrée {(x(t),y(t))}
>>> pp.axis('equal') # Pour que le repère soit orthonormé
>>> pp.title('Le cercle unitaire')
>>> pp.show()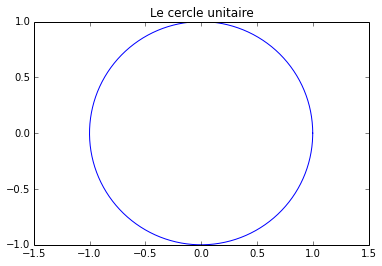

II-C-1. Illustration : approximation de pi▲

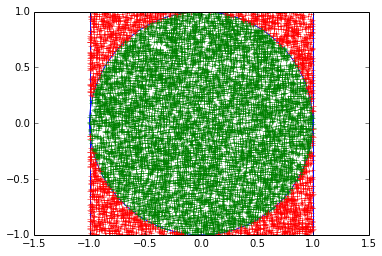
Encore une approximation de kitxmlcodeinlinelatexdvp\pifinkitxmlcodeinlinelatexdvp par une méthode de type Monte-Carlo, mais avec illustration graphique.

On tire au sort N points dans le domaine carré [−1, 1] × [−1, 1] selon une loi uniforme. La probabilité pour un point d'être choisi dans le disque unitaire est égale au quotient de l'aire du disque unitaire par l'aire du domaine carré, soit : kitxmlcodeinlinelatexdvp\dfrac{\pi}{4}finkitxmlcodeinlinelatexdvp

Ainsi d'après le théorème des grands nombres, si l'on tire un grand nombre de points, c'est-à-dire si N est suffisamment grand, la proportion des points tirés se trouvant dans le disque unitaire, avec kitxmlcodeinlinelatexdvpx^2+y^2 \leq 1finkitxmlcodeinlinelatexdvp, est presque sûrement proche de kitxmlcodeinlinelatexdvp\pi / 4finkitxmlcodeinlinelatexdvp.

 

Sélectionnez

import matplotlib.pyplot as pp # pyplot
import numpy as np # numpy
import random as rand # random

def monpi(N):
    X = [rand.uniform(-1,1) for i in range(N)] # choix aléatoire
    Y = [rand.uniform(-1,1) for i in range(N)]
    oui = non = 0 # Calcul de la proportion dans le disque
    for i in range(N):
        if X[i]**2 + Y[i]**2 <= 1:
            oui += 1
        else:
            non += 1
    print 'approximation de pi trouvée :' # impression du résultat
    print 4 * oui / float(oui+non)
    print np.pi
    # Tracé du graphique
    pp.plot([-1,1,1,-1,-1],[-1,-1,1,1,-1], 'b-') # tracé du carré
    T = np.linspace(0,2*np.pi,256)
    Xdisk = np.cos(T)
    Ydisk = np.sin(T)
    pp.plot(Xdisk,Ydisk,'b') # tracé du disque
    for i in range(N): # tracé du nuage de points
        if X[i]**2 + Y[i]**2 <= 1:
            pp.plot([X[i]],[Y[i]], 'g+') # vert si dedans
        else:
            pp.plot([X[i]],[Y[i]], 'r+') # rouge si dehors
    pp.axis('equal')
    pp.show()

 

Sélectionnez

>>> monpi(10000)
approximation de pi trouvée :
3.152
3.14159265359