IV. Corrigés des exercices▲
IV-A. Systèmes linéaires d'équations : solution▲
IV-A-1. système d'équations 1▲
On peut utiliser la fonction solve() du sous-module linalg de NumPy :
import numpy as np
def reponse():
A = np.array([[1,1,1],[1,-2,1],[2,-1,1]])
B = np.array([1,0,2])
return np.linalg.solve(A,B)>>> reponse()
array([ 1.66666667, 0.33333333, -1. ])La solution exacte est kitxmlcodeinlinelatexdvp\begin{pmatrix}\dfrac{5}{3} & \dfrac{1}{3} & -1\end{pmatrix}finkitxmlcodeinlinelatexdvp. En effet les solutions sont rationnelles (car tous les coefficients du système sont entiers), à petit dénominateur (on peut prendre pour dénominateur le déterminant de la matrice du système).
IV-A-2. Système d'équations 2▲
kitxmlcodeinlinelatexdvp\left\{ \begin{array}{r c l} x+y+z &=& a\\ x-2y+z &=& b\\ 2x-y+z &=& c \end{array} \right.finkitxmlcodeinlinelatexdvp avec kitxmlcodeinlinelatexdvp\left\{ \begin{array}{r c l} 3a+b-c &=& 3\\ a+b+c &=& 3\\ a-2b+2c &=& 1 \end{array} \right.finkitxmlcodeinlinelatexdvp
Soit A la matrice du premier système, U = (a; b; c) et X = (x; y; z). Alors, U = A.X
Soit B la matrice du second système et V = (3; 3; 1). Alors, V = B.U
Première solution : à l'aide de solve(). On trouve d'abord U pour en déduire ensuite X :
>>> A = np.array([[1,1,1],[1,-2,1],[2,-1,1]])
>>> B = np.array([[3,1,-1],[1,1,1],[1,-2,2]])
>>> V = np.array([3,3,1])
>>> U = np.linalg.solve(B,V)
>>> np.linalg.solve(A,U)
array([ 0., -0., 1.])Ainsi (0; 0; 1) est solution (remarquer les 0. et -0. apparaissant). La solution est correcte. Avec ces valeurs, on trouve a = b = c = 1 qui est bien solution du deuxième système.
Deuxième solution : à l'aide de inv(). On vérifie que A et B sont inversibles grâce à la fonction det() qui donne le déterminant (A est inversible si, et seulement si, det(A) ≠ 0). Alors, X = A−1U = A−1B−1V
>>> a = np.linalg.inv(A)
>>> b = np.linalg.inv(B)
>>> np.dot(np.dot(a,b),V)
array([ -2.22044605e-16, -1.11022302e-16, 1.00000000e+00]On ne trouve pas la valeur exacte, mais seulement une valeur approchée à 10−15 près. L'inversion des matrices a inséré des erreurs d'arrondis qui se sont propagées et amplifiées. La fonction solve() s'avère plus efficace.
IV-B. Interpolation polynomiale : solution▲
Cela revient à déterminer tous les triplets de réels (a; b; c) tels que le polynôme kitxmlcodeinlinelatexdvpP(x)=a+bx+cx^2finkitxmlcodeinlinelatexdvp prenne les valeurs 1, 4, 3 en 0, 1 et 2. C'est-à-dire les (a; b; c) solutions du système linéaire :
kitxmlcodelatexdvp\left\{ \begin{array}{r c l} a+b.0+c.0^2 &=& 1\\ a+b.1+c.1^2 &=& 4\\ a+b.2+c.2^2 &=& 3 \end{array} \right.finkitxmlcodelatexdvpSoit,
kitxmlcodelatexdvp\left\{ \begin{array}{r c l} a &=& 1\\ a+b+c &=& 4\\ a+2b+4c &=& 3 \end{array} \right.finkitxmlcodelatexdvp>>> A = np.array([[1,0,0],[1,1,1],[1,2,4]])
>>> V = np.array([1,4,3])
>>> np.linalg.solve(A,V)
array([ 1., 5., -2.])Il n'y a qu'une solution : c'est le polynôme kitxmlcodeinlinelatexdvpP(x)=1+5x-2x^2finkitxmlcodeinlinelatexdvp.
IV-C. Tracés avec pyplot : solution▲
Fonction kitxmlcodeinlinelatexdvp\tanfinkitxmlcodeinlinelatexdvp :
>>> import matplotlib.pyplot as pp
>>> import numpy as np
>>> X = np.linspace(-5,5,1000)
>>> Ytan = np.tan(X)
>>> pp.plot(X,Ytan,'b')
>>> pp.grid(True)
>>> pp.show()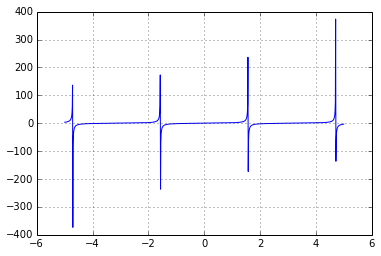
Fonction kitxmlcodeinlinelatexdvp\lnfinkitxmlcodeinlinelatexdvp :
>>> X = np.linspace(0,10,1000)
>>> Yln = np.log(X)
main :1: RuntimeWarning: divide by zero encountered in log
>>> X = X[1:] # Slicing pour éviter le premier nombre, 0.
>>> Yln = np.log(X)
>>> pp.plot(X,Yln,'b')
>>> pp.grid(True)
>>> pp.show()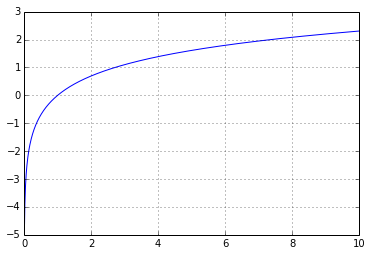
De même pour la fonction kitxmlcodeinlinelatexdvp\dfrac{\sin{x}}{x}finkitxmlcodeinlinelatexdvp :
>>> X = np.linspace(0,10,1000)
>>> X = X[1:] # Slicing pour éviter le premier nombre, 0.
>>> Y = [np.sin(x)/float(x) for x in X]
>>> pp.plot(X,Y)
>>> pp.grid(True)
>>> pp.show()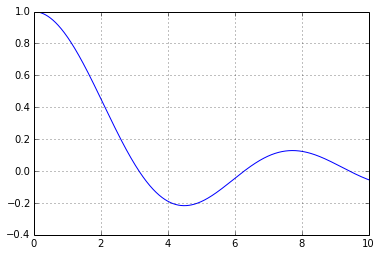
Tracé de la courbe paramétrée :
kitxmlcodeinlinelatexdvpx(t)=t \cdot \cos(t) , \: y(t)=t \cdot \sin(t)finkitxmlcodeinlinelatexdvp pour kitxmlcodeinlinelatexdvpt \in [0, 10]finkitxmlcodeinlinelatexdvp
>>> import numpy as np
>>> import matplotlib.pyplot as pp
>>> T = np.linspace(0,10,256)
>>> X = T * np.cos(T)
>>> Y = T * np.sin(T)
>>> pp.plot(X,Y,'b')
>>> pp.grid(True)
>>> pp.axis('equal')
>>> pp.show()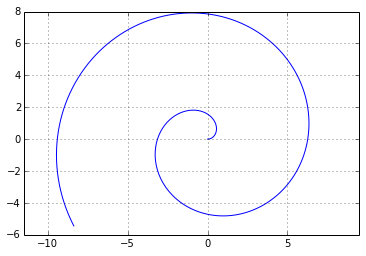
Pour une ellipse :
>>> a = 2; b = 1
>>> T = np.linspace(0,2*np.pi,1000)
>>> pp.plot(a*np.cos(T),b*np.sin(T),'b')
>>> pp.grid(True)
>>> pp.show()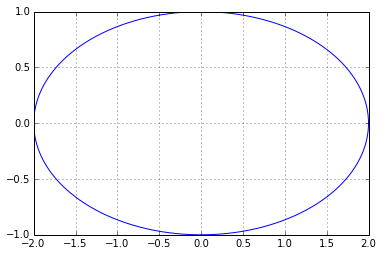
IV-D. Calcul d'aire d'une ellipse : solution▲
De l'équation kitxmlcodeinlinelatexdvp\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1finkitxmlcodeinlinelatexdvp découle que les parties supérieure et inférieure de l'ellipse ont pour équation kitxmlcodeinlinelatexdvpy = \pm \dfrac{b}{a} \sqrt{a^2-x^2}finkitxmlcodeinlinelatexdvp.
Ainsi l'aire de l'ellipse est :
kitxmlcodelatexdvpA = \dfrac{2b}{a} \int^a_{-a} \sqrt{a^2-x^2}\textrm{d}xfinkitxmlcodelatexdvpIV-E. Tracé du graphe de la dérivée d'une fonction : solution▲
def derive(f,x,h): # Calcul approché de la dérivée en 1 point
return (f(x+h)-f(x-h))/float(2*h)
import numpy as np
import matplotlib.pyplot as pp
def trace(f,a,b):
N = 100
X = np.linspace(a,b,N)
Yf = f(X)
Yd = np.empty(N) # tableau vide de N éléments
for i in range(N):
Yd[i] = derive(f,X[i],0.01)
pp.plot(X,Yf,'b',X,Yd,'r')
pp.grid(True)
pp.legend(('fonction','derivée'),'lower right')
pp.show()En utilisant le calcul sur les tableaux, plutôt qu'en calculant la dérivée en chaque point à l'aide d'une boucle for.
def derive(f,x,h=0.01): # Calcul approché de la dérivée
return (f(x+h)-f(x-h))/float(2*h)
import numpy as np
import matplotlib.pyplot as pp
def trace(f,a,b):
N = 100
X = np.linspace(a,b,N)
Yf = f(X)
Yd = np.empty(N)
Yd = derive(f,X) # Le 2e argument passé est un tableau
pp.plot(X,Yf,'b',X,Yd,'r')
pp.grid(True)
pp.legend(('fonction','derivée'),'lower right')
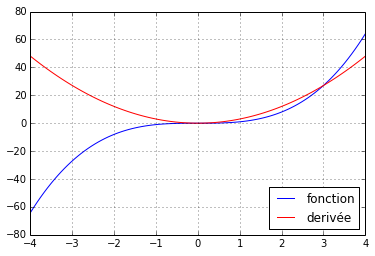
pp.show()>>> f = lambda x: x**3
>>> trace(f,-4,4)Tracé des graphes de kitxmlcodeinlinelatexdvpf\,:\,x\mapsto x^3finkitxmlcodeinlinelatexdvp et de sa dérivée kitxmlcodeinlinelatexdvpf'\,:\,x\mapsto 3x^2finkitxmlcodeinlinelatexdvp sur [−4, 4] :